看见函数

　　看到函数公式app，协助你随时随地学习培训变量的数学思维学习软件。在看到函数公式app中你可以轻轻松松测算、学习培训指数函数、对数函数和对数函数，线上制作函数方程绘制函数曲线等。

基本上介绍

　　看到函数公式app依据客户键入的函数方程制作函数曲线。

　　看到函数公式app适用加、减、乘、除、指数函数、对数函数、对数函数、三角函数，反三角函数等全部初等函数。此外看到函数公式app还适用平方根、最少、较大等函数公式。

　　除此之外在看到函数公式app制作的函数曲线可以移动和调整图片大小，且变大时最少座标企业为0.001。

有关详细介绍

　　函数公式(function)，最开始由我国清代数学家李善兰翻译工作，出自于其作品《代数学》。往往那么翻译工作，他提供的因素是“凡此变化中函彼变数者，则其为彼之函数公式”，也即函数指一个量伴随另一个量的变动而转变，换句话说一个量中包括另一个量。函数的概念通常分成传统式界定和近现代界定，函数公式的2个界定实质是一致的，仅仅描述定义的立足点不一样，传统式界定是以健身运动转变的思想观点考虑，而近现代界定是以结合、投射的思想观点考虑。

　　函数公式的来历

　　汉语数学思维书上应用的“函数公式”一词是转译词。是中国清朝数学家李善兰在翻译《代数学》(1859年)一书时，把“function”翻译成“函数公式”的。

　　古代中国“函”字与“含”字通用性，都拥有“包括”的含意。李善兰得出的界定是：“凡式中含天，为天下函数公式。”古代中国用天、地、人、物4个字来表明4个不一样的未知量或自变量。这一界定的含意是：“只要是公式计算中带有自变量x，则该算式称为x的函数公式。”因此“函数公式”就是指公式计算里带有自变量的含意。大家所指的方程式的准确界定就是指带有未知量的式子。可是方程式一词在中国初期的数学专著《九章算术》中，含意指的是包括好几个未知量的联立方程一次方程，即常说的线性微分方程。

　　函数定义

　　传统式界定

　　一般的，在一个转变历程中，假定有两个自变量 x、y ，假如针对随意一个 x 都是有唯一明确的一个 y 和它相匹配，那麼就称 x 是变量，y 是 x 的函数公式。x的取值范围称为这一函数的定义域，相对应 y 的取值范围称为函数的值域。

　　近现代界定

　　设 A，B 是是非非空 的数集，假如依照某类明确的对应关系 f ，使针对结合 A 中的随意一个数 x ，在结合B里都有唯一明确的数 y 和它相匹配，那麼就称投射 f ：A → B 为从结合A到集合B的一个函数公式，记作：

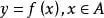
　　或

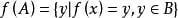
　　在其中x称为变量， y 称为 x 的函数公式，结合A

　　称为函数的定义域，与 x 相匹配的 y 称为函数，函数值的结合

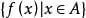
　　称为函数的值域，f 叫做对应法则。在其中，函数定义域、函数值域和对应法则被称作函数三要素。函数定义域，函数值域，对应法则称之为函数公式的三要素。一般撰写为：

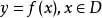
　　若省去函数定义域，一般是挑唆函数公式更有意义的结合。

升级日志